INTEGRAL FUNGSI RASIONAL QUIZ
Assalamu'alaikum Wr.wb, hai guys setelah kita membahas mengenai integral fungsi rasional pada link sebelumnya, kini saatnya saya akan menguji pengetahuan kalian dengan beberapa soal yang berkaitan dengan pembahasan yang telah dipaparkan. Silahkan klik link dibawah ini:
https://docs.google.com/forms/d/1DTKHCSKrVbwfVtizwkBgs3AjaZdWin54esnJFRGVO00/edit?usp=drivesdk
Sabtu, 11 Juli 2020
Integral Fungsi Rasional 2
Assalamu'alaikum Wr wb, pada pembahasan kali ini penulis akan melanjutkan pembahasan mengenai "Integral Fungsi Rasional 2" yang masih ada kaitanya dengan pembahasan sebelumnya.
INTEGRAL FUNGSI RASIONAL
Pada pembahasan sebelumnya, kita sudah membahas mengenai definisi fungsi rasional serta dekomposisi pecahan parsial, kedua materi tersebut akan sangat berguna dalam memecahkan segala macam integral. Dalam menyelesaikan integral fungsi rasional, terdapat beberapa teknik dalam mengerjakannya, yaitu:
A. Menggunakan Cara Substitusi
B. Menggunakan Pecahan Parsial
C. Menggunakan Cara Pembagian Menurun
A. Menggunakan Cara Substitusi
Metode ini merupakan cara yang sudah biasa dalam mengerjakan integral fungsi rasional yaitu cukup dengan memisalkan fungsi yang dipilih dengan variabel apa saja agar fungsi menjadi mudah untuk diintegralkan. Metode ini ada 2 jenis yaitu substitusi langsung dan substitusi trigonometri, substitusi langsung dapat dilakukan dengan cara memisalkan fungsi kedalam variabel apa saja agar mudah diintegralkan, sementara substitusi trigonometri dapat dilakukan dengan cara mensubstitusi variabel dalam fungsi menjadi bentuk trigonometri, biasanya cara ini dipakai apabila dengan metode substitusi langsung tidak bisa diselesaikan. Kita ambil salah satu contoh saja.
Contoh 1:
Selesaikanlah
!
Jawab:
Dengan mencoba menurunkan fungsi pada penyebut, kita akan mengetahui bahwa turunannya akan sama dengan fungsi pada pembilangnya yang artinya bahwa fungsi rasional tersebut dapat diselesaikan dengan substitusi langsung.
Misalkan:
Substitusikan saja ini ke fungsi semula, maka:
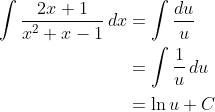
Kembalikan u dalam x sehingga diperolehlah solusi integralnya, jadi:
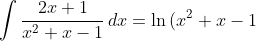}+C "\int{\frac{2x+1}{x^2+x-1}\,dx}=\ln{(x^2+x-1)}+C")
B. Menggunakan Pecahan Parsial
Metode ini adalah metode yang sedikit lebih kompleks untuk sebagian orang yaitu metode pecahan parsial, pembahasan pecahan parsial telah dijelaskan pada bagian sebelumnya. Penyelesaian dengan metode ini dapat dilakukan apabila cara yang diuraikan pada bagian A tidak berhasil kita lakukan. Kita ambil satu contoh soal saja untuk kasus ini.
Contoh 2:
Selesaikanlah
!
Jawab:
Apabila kita turunkan pada bagian penyebut, kita bisa melihat bahwa hasil turunannya tidak sama dengan fungsi dibagian pembilangnya yang berarti bahwa fungsi tersebut tidak bisa kita selesaikan dengan metode A sehingga kita memerlukan metode lain, yaitu pecahan parsial. Agar fungsi tersebut dapat kita ubah kedalam pecahan-pecahan parsial, kita harus menguraikan fungsi pada bagian penyebut menjadi perkalian beberapa fungsi. Telah kita ketahui bersama bahwa faktor dari polinomial tersebut adalah 1/2, maka fungsi tersebut bisa uraikan menjadi:
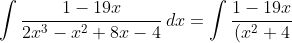(2x-1)}\,dx} "\int{\frac{1-19x}{2x^3-x^2+8x-4}\,dx}=\int{\frac{1-19x}{(x^2+4)(2x-1)}\,dx}")
Perhatikan ! Disini kita mendapatkan dua fungsi yaitu fungsi kuadrat dan fungsi linear, maka dekomposisinya kemungkinan campuran antara aturan 1 dan 2 (lihat pembahasan sebelumnya), sehingga:
(2x-1)}\,dx}\\&space;&=\int{\left(\frac{Ax+B}{x^2+4}+\frac{C}{2x-1}\right)\,dx}\end{aligned} "\begin{aligned} \int{\frac{1-19x}{2x^3-x^2+8x-4}\,dx}&=\int{\frac{1-19x}{(x^2+4)(2x-1)}\,dx}\\ &=\int{\left(\frac{Ax+B}{x^2+4}+\frac{C}{2x-1}\right)\,dx}\end{aligned}")
Lakukan seperti Contoh-contoh pada bahasan sebelumnya yaitu "Integral Fungsi Rasional 1" dan jika dilakukan dengan benar anda akan memperoleh A = 1, B = -9, dan C = -2. Dengan mengganti nilai masing-masing, diperolehlah hasil dekomposisinya, sehingga:
(2x-1)}\,dx}\\&space;&=\int{\left(\frac{x-9}{x^2+4}-\frac{2}{2x-1}\right)\,dx}\\&space;&=\int{\frac{x}{x^2+4}\,dx}-\int{\frac{9}{x^2+4}\,dx}-\int{\frac{2}{2x-1}\,dx}\end{aligned} "\begin{aligned} \int{\frac{1-19x}{2x^3-x^2+8x-4}\,dx}&=\int{\frac{1-19x}{(x^2+4)(2x-1)}\,dx}\\ &=\int{\left(\frac{x-9}{x^2+4}-\frac{2}{2x-1}\right)\,dx}\\ &=\int{\frac{x}{x^2+4}\,dx}-\int{\frac{9}{x^2+4}\,dx}-\int{\frac{2}{2x-1}\,dx}\end{aligned}")
Terlihat bahwa bentuk integral yang tadinya terlihat kompleks sekarang menjadi pengurangan beberapa integral pecahan yang sederhana, selanjutnya tinggal kita selesaikan setiap integral tersebut.
}+C_1\\&space;\int{\frac{9}{x^2+4}\,dx}&=\frac{9}{2}\arctan{\frac{1}{2}x}+C_2\\&space;\int{\frac{2}{2x-1}\,dx}&=\ln{(2x-1)}+C_3\end{aligned} "\begin{aligned} \int{\frac{x}{x^2+4}\,dx}&=\frac{1}{2}\ln{(x^2+4)}+C_1\\ \int{\frac{9}{x^2+4}\,dx}&=\frac{9}{2}\arctan{\frac{1}{2}x}+C_2\\ \int{\frac{2}{2x-1}\,dx}&=\ln{(2x-1)}+C_3\end{aligned}")
Jadi,
}+C_1\right)-\left(\frac{9}{2}\arctan{\frac{1}{2}x}+C_2\right)-\left(\ln{(2x-1)}+C_3\right)\\&space;&=\frac{1}{2}\ln{(x^2+4)}-\frac{9}{2}\arctan{\frac{1}{2}x}-\ln{(2x-1)}+C\end{aligned} "\begin{aligned}&space;\int{\frac{1-19x}{2x^3-x^2+8x-4}\,dx}&=\left(\frac{1}{2}\ln{(x^2+4)}+C_1\right)-\left(\frac{9}{2}\arctan{\frac{1}{2}x}+C_2\right)-\left(\ln{(2x-1)}+C_3\right)\\&space;&=\frac{1}{2}\ln{(x^2+4)}-\frac{9}{2}\arctan{\frac{1}{2}x}-\ln{(2x-1)}+C\end{aligned}")
C. Menggunakan Cara Pembagian Menurun
Apabila derajat fungsi pembilang lebih besar dari derajat fungsi penyebut, maka menggunakan metode A maupun B akan sangat sulit untuk memecahkannya, sehingga untuk kasus seperti ini, kita bisa menggunakan metode pembagian menurun seperti kita membagi bilangan di Sekolah Dasar dan ditambah dengan sisa pembagi.
Dalil:
Jika diberikan suatu integral fungsi rasional dimana derajat fungsi pembilang P(x) lebih besar dari penyebut Q(x), maka:
}{Q(x)}\,dx}=\int{\left(R(x)+\frac{S(x)}{Q(x)}\right)\,dx} "\int{\frac{P(x)}{Q(x)}\,dx}=\int{\left(R(x)+\frac{S(x)}{Q(x)}\right)\,dx}")
Dengan;
R(x): Hasil bagi
Q(x): Pembagi
S(x): Sisa pembagian
Contoh 3:
Selesaikanlah
!
Jawab:
Soal tersebut sangat jelas tidak dapat kita substitusi dengan fungsi apapun, di sisi lain bentuk tersebut juga tidak dapat kita uraikan dengan dekomposisi pecahan parsial, maka hal yang mungkin kita lakukan untuk mereduksi fungsi tersebut yaitu dengan melakukan pembagian antara pembilang dengan penyebut lalu meletakkan hasilnya dibagian pembilang seperti yang ditunjukkan pada nomor 1 dibawah,pembagian dilakukan dengan cara menurun, dengan begitu kita akan memperoleh:
(x^2+3)+(4-3x)}{x^2+3}}...(1)\\&space;&=\int{\left((x-1)+\frac{4-3x}{x^2+3}\right)}\end{aligned} "\begin{aligned} \int{\frac{x^3-x^2+1}{x^2+3}\,dx}&=\int{\frac{(x-1)(x^2+3)+(4-3x)}{x^2+3}}...(1)\\ &=\int{\left((x-1)+\frac{4-3x}{x^2+3}\right)}\end{aligned}")
Selanjutnya, kita pecah menjadi integral-integral yang sederhana.
+\frac{4-3x}{x^2+3}\right)\,dx}\\&space;&=\int{(x-1)\,dx}+\int{\frac{4-3x}{x^2+3}\,dx}\\&space;&=\int{(x-1)\,dx}+\int{\frac{4}{x^2+3}\,dx}-\int{\frac{3x}{x^2+3}\,dx}\end{aligned} "\begin{aligned} \int{\frac{x^3-x^2+1}{x^2+3}\,dx}&=\int{\left((x-1)+\frac{4-3x}{x^2+3}\right)\,dx}\\ &=\int{(x-1)\,dx}+\int{\frac{4-3x}{x^2+3}\,dx}\\ &=\int{(x-1)\,dx}+\int{\frac{4}{x^2+3}\,dx}-\int{\frac{3x}{x^2+3}\,dx}\end{aligned}")
Sekarang, kita sudah bisa mengintegralkannya masing-masing, sehingga nantinya akan diperoleh:
\,dx}&=\frac{1}{2}x^2-x+C_1\\&space; \int{\frac{4}{x^2+3}\,dx}&=\frac{4}{3}\sqrt{3}\arctan{\frac{1}{3}x\sqrt{3}}+C_2\\&space; \int{\frac{3x}{x^2+3}\,dx}&=\frac{3}{2}\ln{(x^2+3)}+C_3\end{aligned} "\begin{aligned}&space; \int{(x-1)\,dx}&=\frac{1}{2}x^2-x+C_1\\&space; \int{\frac{4}{x^2+3}\,dx}&=\frac{4}{3}\sqrt{3}\arctan{\frac{1}{3}x\sqrt{3}}+C_2\\&space; \int{\frac{3x}{x^2+3}\,dx}&=\frac{3}{2}\ln{(x^2+3)}+C_3\end{aligned}")
Jadi,
+\left(\frac{4}{3}\sqrt{3}\arctan{\frac{1}{3}x\sqrt{3}}+C_2\right)-\left(\frac{3}{2}\ln{(x^2+3)}+C_3\right)\\&space; &=\frac{1}{2}x^2-x+\frac{4}{3}\sqrt{3}\arctan{\frac{1}{3}x\sqrt{3}}-\frac{3}{2}\ln{(x^2+3)}+C\end{aligned} "\begin{aligned}&space; \int{\frac{x^3-x^2+1}{x^2+3}\,dx}&=\left(\frac{1}{2}x^2-x+C_1\right)+\left(\frac{4}{3}\sqrt{3}\arctan{\frac{1}{3}x\sqrt{3}}+C_2\right)-\left(\frac{3}{2}\ln{(x^2+3)}+C_3\right)\\&space; &=\frac{1}{2}x^2-x+\frac{4}{3}\sqrt{3}\arctan{\frac{1}{3}x\sqrt{3}}-\frac{3}{2}\ln{(x^2+3)}+C\end{aligned}")
Demikianlah untuk pembahasan mengenai "Integral Fungsi Rasional 2" jika dalam penulisan ini masih terdapat banyak kekurangan penulis mohon maaf yang sebesar-besarnya dan apabila ada yang belum mengerti silahkan tanyakan di kolom komentar. Wa'ssalam.
INTEGRAL FUNGSI RASIONAL
Pada pembahasan sebelumnya, kita sudah membahas mengenai definisi fungsi rasional serta dekomposisi pecahan parsial, kedua materi tersebut akan sangat berguna dalam memecahkan segala macam integral. Dalam menyelesaikan integral fungsi rasional, terdapat beberapa teknik dalam mengerjakannya, yaitu:
A. Menggunakan Cara Substitusi
B. Menggunakan Pecahan Parsial
C. Menggunakan Cara Pembagian Menurun
A. Menggunakan Cara Substitusi
Metode ini merupakan cara yang sudah biasa dalam mengerjakan integral fungsi rasional yaitu cukup dengan memisalkan fungsi yang dipilih dengan variabel apa saja agar fungsi menjadi mudah untuk diintegralkan. Metode ini ada 2 jenis yaitu substitusi langsung dan substitusi trigonometri, substitusi langsung dapat dilakukan dengan cara memisalkan fungsi kedalam variabel apa saja agar mudah diintegralkan, sementara substitusi trigonometri dapat dilakukan dengan cara mensubstitusi variabel dalam fungsi menjadi bentuk trigonometri, biasanya cara ini dipakai apabila dengan metode substitusi langsung tidak bisa diselesaikan. Kita ambil salah satu contoh saja.
Contoh 1:
Selesaikanlah
Jawab:
Dengan mencoba menurunkan fungsi pada penyebut, kita akan mengetahui bahwa turunannya akan sama dengan fungsi pada pembilangnya yang artinya bahwa fungsi rasional tersebut dapat diselesaikan dengan substitusi langsung.
Misalkan:
Substitusikan saja ini ke fungsi semula, maka:
Kembalikan u dalam x sehingga diperolehlah solusi integralnya, jadi:
B. Menggunakan Pecahan Parsial
Metode ini adalah metode yang sedikit lebih kompleks untuk sebagian orang yaitu metode pecahan parsial, pembahasan pecahan parsial telah dijelaskan pada bagian sebelumnya. Penyelesaian dengan metode ini dapat dilakukan apabila cara yang diuraikan pada bagian A tidak berhasil kita lakukan. Kita ambil satu contoh soal saja untuk kasus ini.
Contoh 2:
Selesaikanlah
Jawab:
Apabila kita turunkan pada bagian penyebut, kita bisa melihat bahwa hasil turunannya tidak sama dengan fungsi dibagian pembilangnya yang berarti bahwa fungsi tersebut tidak bisa kita selesaikan dengan metode A sehingga kita memerlukan metode lain, yaitu pecahan parsial. Agar fungsi tersebut dapat kita ubah kedalam pecahan-pecahan parsial, kita harus menguraikan fungsi pada bagian penyebut menjadi perkalian beberapa fungsi. Telah kita ketahui bersama bahwa faktor dari polinomial tersebut adalah 1/2, maka fungsi tersebut bisa uraikan menjadi:
Perhatikan ! Disini kita mendapatkan dua fungsi yaitu fungsi kuadrat dan fungsi linear, maka dekomposisinya kemungkinan campuran antara aturan 1 dan 2 (lihat pembahasan sebelumnya), sehingga:
Lakukan seperti Contoh-contoh pada bahasan sebelumnya yaitu "Integral Fungsi Rasional 1" dan jika dilakukan dengan benar anda akan memperoleh A = 1, B = -9, dan C = -2. Dengan mengganti nilai masing-masing, diperolehlah hasil dekomposisinya, sehingga:
Terlihat bahwa bentuk integral yang tadinya terlihat kompleks sekarang menjadi pengurangan beberapa integral pecahan yang sederhana, selanjutnya tinggal kita selesaikan setiap integral tersebut.
Jadi,
C. Menggunakan Cara Pembagian Menurun
Apabila derajat fungsi pembilang lebih besar dari derajat fungsi penyebut, maka menggunakan metode A maupun B akan sangat sulit untuk memecahkannya, sehingga untuk kasus seperti ini, kita bisa menggunakan metode pembagian menurun seperti kita membagi bilangan di Sekolah Dasar dan ditambah dengan sisa pembagi.
Dalil:
Jika diberikan suatu integral fungsi rasional dimana derajat fungsi pembilang P(x) lebih besar dari penyebut Q(x), maka:
Dengan;
R(x): Hasil bagi
Q(x): Pembagi
S(x): Sisa pembagian
Contoh 3:
Selesaikanlah
Jawab:
Soal tersebut sangat jelas tidak dapat kita substitusi dengan fungsi apapun, di sisi lain bentuk tersebut juga tidak dapat kita uraikan dengan dekomposisi pecahan parsial, maka hal yang mungkin kita lakukan untuk mereduksi fungsi tersebut yaitu dengan melakukan pembagian antara pembilang dengan penyebut lalu meletakkan hasilnya dibagian pembilang seperti yang ditunjukkan pada nomor 1 dibawah,pembagian dilakukan dengan cara menurun, dengan begitu kita akan memperoleh:
Selanjutnya, kita pecah menjadi integral-integral yang sederhana.
Sekarang, kita sudah bisa mengintegralkannya masing-masing, sehingga nantinya akan diperoleh:
Jadi,
Demikianlah untuk pembahasan mengenai "Integral Fungsi Rasional 2" jika dalam penulisan ini masih terdapat banyak kekurangan penulis mohon maaf yang sebesar-besarnya dan apabila ada yang belum mengerti silahkan tanyakan di kolom komentar. Wa'ssalam.
Jumat, 10 Juli 2020
Integral Fungsi Rasional 1
Assalamu'alaikum Wr wb, pada bahasan kali ini penulis akan mengulas salah satu materi matematika yang berjudul "Integral Fungsi Rasional 1" yang masih berkaitan dengan pecahan parsial, sebelum kita membahas mengenai materi tersebut, alangkah baiknya dengan terlebih dahulu membahas apa yang dimaksud dengan fungsi rasional tersebut.
A. DEFINISI FUNGSI RASIONAL
Fungsi rasional adalah fungsi yang berbentuk pecahan, biasanya ditulis sebagai:
}{g(x)} "y=\frac{f(x)}{g(x)}")
, dengan g(x) ≠ 0 dan f(x) ≠ 0
Grafik fungsi rasional umumnya berbentuk seperti hiperbola, berikut contoh dari fungsi rasional:
}^2} "y=\frac{1}{{(x-1)}^2}")
B. PECAHAN PARSIAL
Misalkan diberikan sebuah penjumlahan dua buah fungsi rasional berikut.
Jika kita samakan penyebutnya kemudian bagian pembilang kita jumlahkan. Kita akan memperoleh bentuk:
}{x+1}+\frac{2(x+1)}{x-2}\\&space;&=\frac{3x-6}{x+1}+\frac{2x+2}{x-2}\\&space;&=\frac{5x-4}{(x+1)(x-2)}\cdots(1)\end{aligned} "\begin{aligned} \frac{3}{x+1}+\frac{2}{x-2}&=\frac{3(x-2)}{x+1}+\frac{2(x+1)}{x-2}\\ &=\frac{3x-6}{x+1}+\frac{2x+2}{x-2}\\ &=\frac{5x-4}{(x+1)(x-2)}\cdots(1)\end{aligned}")
Apabila kita misalkan A = 3 dan B = 2 dan mengambil bentuk terakhir dari persamaan (1) tersebut, maka:
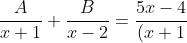(x-2)}\cdots(2) "\frac{A}{x+1}+\frac{B}{x-2}=\frac{5x-4}{(x+1)(x-2)}\cdots(2)")
Sehingga, bentuk (2) inilah yang disebut sebagai dekomposisi pecahan parsial. Bentuk dari dekomposisi bisa berbeda berbeda tergantung kondisi dari bentuk persamaan tersebut. Dekomposisi sendiri terdapat beberapa kondisi, yaitu:
1. Apabila Faktor Penyebut Linear
Apabila faktor penyebut berbentuk linear, maka pembilang dari pecahan tersebut adalah konstanta sehingga bentuk dekomposisinya:
}{g(x)}=\frac{A}{h(x)} "\frac{f(x)}{g(x)}=\frac{A}{h(x)}")
2. Apabila Faktor Penyebut Berbentuk Polinomial
Apabila faktor penyebut berbentuk polinomial (suku banyak), maka bentuk dekomposisinya tergantung derajat sukunya.
}{g(x)}=\frac{ax^{n-1}+bx^{n-2}+cx^{n-3}+...+k}{px^{n}+qx^{n-1}+rx^{n-2}+...+t} "\frac{f(x)}{g(x)}=\frac{ax^{n-1}+bx^{n-2}+cx^{n-3}+...+k}{px^{n}+qx^{n-1}+rx^{n-2}+...+t}")
3. Apabila Faktor Penyebut Berulang
Untuk kasus faktor berulang, bentuk dekomposisinya adalah:
}{{(g(x))}^n}=\frac{h_1(x)}{{(g(x))}^n}+\frac{h_2(x)}{{(g(x))}^{n-1}}+\frac{h_3(x)}{{(g(x))}^{n-2}}+... "\frac{f(x)}{{(g(x))}^n}=\frac{h_1(x)}{{(g(x))}^n}+\frac{h_2(x)}{{(g(x))}^{n-1}}+\frac{h_3(x)}{{(g(x))}^{n-2}}+...")
Adakalanya bentuknya campuran antara 1, 2, atau 3. Maka, bentuk dekomposisinya tinggal disesuaikan saja dengan melihat bentuk dipenyebutnya apabila penyebutnya berbentuk linear maka gunakan bentuk 1, bila polinomial gunakan bentuk 2, dan bila berulang tetap gunakan aturan 3 sekaligus aturan 1 atau 2. Untuk lebih jelasnya, perhatikan beberapa contoh dibawah ini.
Contoh 1:
Ubah bentuk(x-1)} "y=\frac{5x-1}{(x+3)(x-1)}")
menjadi penjumlahan pecahan parsial !
Jawab:
Jika kita perhatikan, penyebut pada fungsi tersebut adalah linear, maka kita bisa menggunakan aturan 1 untuk dekomposisinya, karena ada 2 fungsi pada bagian penyebut, maka kita bisa memisalkan konstanta di pembilang masing-masing A dan B. Sehingga:
(x-1)}\\&space;&=\frac{A}{x+3}+\frac{B}{x-1}\end{aligned} "\begin{aligned} y&=\frac{5x-1}{(x+3)(x-1)}\\ &=\frac{A}{x+3}+\frac{B}{x-1}\end{aligned}")
Dengan menyamakan penyebutnya, lalu mengaitkannya ke fungsi semula. Kita memperoleh:
(x-1)}&=\frac{A(x-1)}{(x+3)(x-1)}+\frac{B(x+3)}{(x+3)(x-1)}\\&space;&=\frac{Ax-A+Bx+3B}{(x+3)(x-1)}\\&space;&=\frac{(A+B)x+(3B-A)}{(x+3)(x-1)}\end{aligned} "\begin{aligned}&space;\frac{5x-1}{(x+3)(x-1)}&=\frac{A(x-1)}{(x+3)(x-1)}+\frac{B(x+3)}{(x+3)(x-1)}\\&space;&=\frac{Ax-A+Bx+3B}{(x+3)(x-1)}\\&space;&=\frac{(A+B)x+(3B-A)}{(x+3)(x-1)}\end{aligned}")
Dari sini, dengan menggunakan kesamaan antara ruas kiri dan kanan, akan diperoleh dua buah persamaan linear. Yaitu:
\\3B-A=-1...(2)\end{matrix}\right. "\left\{\begin{matrix}A+B=5...(1)\\3B-A=-1...(2)\end{matrix}\right.")
Selesaikan sistem persamaan tersebut dan jika dilakukan dengan benar anda akan memperoleh A = 4 dan B = 1. Sebagai akibatnya, jika kedua nilai tersebut disubstitusi ke proses yang pertama kali kita lakukan, maka fungsi akan berubah menjadi:
(x-1)}\\&space;&=\frac{4}{x+3}+\frac{1}{x-1}\end{aligned} "\begin{aligned} y&=\frac{5x-1}{(x+3)(x-1)}\\ &=\frac{4}{x+3}+\frac{1}{x-1}\end{aligned}")
Sehingga telah berhasilah kita mengubah fungsi tersebut ke dalam penjumlahan pecahan-pecahan parsial.
Contoh 2:
Nyatakan bentuk(x+2)} "y=\frac{x-3}{(x^2+1)(x+2)}")
ke dalam penjumlahan pecahan-pecahan parsial !
Jawab:
Dengan menganalisa fungsi tersebut, kita dapat melihat bahwa fungsi rasional tersebut berbentuk campuran antara linear dan polinomial, seperti keterangan sebelumnya, jika berbentuk campuran maka mendekomposisikanya hanya dengan menyesuaikan dengan persamaan di penyebutnya. Untuk fungsi polinomial, gunakanlah bentuk 2 dan jika linear, gunakan bentuk 1. Karena fungsi polinomial tersebut berderajat 2 dan salah satu persamaan adalah linear, maka bentuk dekomposisinya:
(x+2)}\\&space;&=\frac{Ax+B}{x^2+1}+\frac{C}{x+2}\end{aligned} "\begin{aligned}&space;y&=\frac{x-3}{(x^2+1)(x+2)}\\&space;&=\frac{Ax+B}{x^2+1}+\frac{C}{x+2}\end{aligned}")
Dengan cara yang sama seperti pada contoh 1, akan diperoleh A = 1, B = -1, dan C = -1 sehingga bentuk dekomposisi dari y adalah:
Demikianlah untuk pembahasan mengenai "Integral Fungsi Rasional 1" sedangkan untuk bagian kedua dari pembahasan tersebut akan penulis posting di lain kesempatan, jika dalam penulisan ini masih terdapat banyak kekurangan penulis mohon maaf yang sebesar-besarnya dan apabila ada yang belum mengerti silahkan tanyakan di kolom komentar. Wa'ssalam.
A. DEFINISI FUNGSI RASIONAL
Fungsi rasional adalah fungsi yang berbentuk pecahan, biasanya ditulis sebagai:
Grafik fungsi rasional umumnya berbentuk seperti hiperbola, berikut contoh dari fungsi rasional:
B. PECAHAN PARSIAL
Misalkan diberikan sebuah penjumlahan dua buah fungsi rasional berikut.
Jika kita samakan penyebutnya kemudian bagian pembilang kita jumlahkan. Kita akan memperoleh bentuk:
Apabila kita misalkan A = 3 dan B = 2 dan mengambil bentuk terakhir dari persamaan (1) tersebut, maka:
Sehingga, bentuk (2) inilah yang disebut sebagai dekomposisi pecahan parsial. Bentuk dari dekomposisi bisa berbeda berbeda tergantung kondisi dari bentuk persamaan tersebut. Dekomposisi sendiri terdapat beberapa kondisi, yaitu:
1. Apabila Faktor Penyebut Linear
Apabila faktor penyebut berbentuk linear, maka pembilang dari pecahan tersebut adalah konstanta sehingga bentuk dekomposisinya:
2. Apabila Faktor Penyebut Berbentuk Polinomial
Apabila faktor penyebut berbentuk polinomial (suku banyak), maka bentuk dekomposisinya tergantung derajat sukunya.
3. Apabila Faktor Penyebut Berulang
Untuk kasus faktor berulang, bentuk dekomposisinya adalah:
Adakalanya bentuknya campuran antara 1, 2, atau 3. Maka, bentuk dekomposisinya tinggal disesuaikan saja dengan melihat bentuk dipenyebutnya apabila penyebutnya berbentuk linear maka gunakan bentuk 1, bila polinomial gunakan bentuk 2, dan bila berulang tetap gunakan aturan 3 sekaligus aturan 1 atau 2. Untuk lebih jelasnya, perhatikan beberapa contoh dibawah ini.
Contoh 1:
Ubah bentuk
Jawab:
Jika kita perhatikan, penyebut pada fungsi tersebut adalah linear, maka kita bisa menggunakan aturan 1 untuk dekomposisinya, karena ada 2 fungsi pada bagian penyebut, maka kita bisa memisalkan konstanta di pembilang masing-masing A dan B. Sehingga:
Dengan menyamakan penyebutnya, lalu mengaitkannya ke fungsi semula. Kita memperoleh:
Dari sini, dengan menggunakan kesamaan antara ruas kiri dan kanan, akan diperoleh dua buah persamaan linear. Yaitu:
Selesaikan sistem persamaan tersebut dan jika dilakukan dengan benar anda akan memperoleh A = 4 dan B = 1. Sebagai akibatnya, jika kedua nilai tersebut disubstitusi ke proses yang pertama kali kita lakukan, maka fungsi akan berubah menjadi:
Sehingga telah berhasilah kita mengubah fungsi tersebut ke dalam penjumlahan pecahan-pecahan parsial.
Contoh 2:
Nyatakan bentuk
Jawab:
Dengan menganalisa fungsi tersebut, kita dapat melihat bahwa fungsi rasional tersebut berbentuk campuran antara linear dan polinomial, seperti keterangan sebelumnya, jika berbentuk campuran maka mendekomposisikanya hanya dengan menyesuaikan dengan persamaan di penyebutnya. Untuk fungsi polinomial, gunakanlah bentuk 2 dan jika linear, gunakan bentuk 1. Karena fungsi polinomial tersebut berderajat 2 dan salah satu persamaan adalah linear, maka bentuk dekomposisinya:
Dengan cara yang sama seperti pada contoh 1, akan diperoleh A = 1, B = -1, dan C = -1 sehingga bentuk dekomposisi dari y adalah:
Demikianlah untuk pembahasan mengenai "Integral Fungsi Rasional 1" sedangkan untuk bagian kedua dari pembahasan tersebut akan penulis posting di lain kesempatan, jika dalam penulisan ini masih terdapat banyak kekurangan penulis mohon maaf yang sebesar-besarnya dan apabila ada yang belum mengerti silahkan tanyakan di kolom komentar. Wa'ssalam.
Video
Ini video tentang integral fungsi rasional, mohon maaf dengan kualitas video rendah karena file ini hasil kompres kalau yang asli sangat besar.
Kamis, 14 Mei 2020
Cara Mudah Menjumlahkan Bilangan Heksadesimal
Cara Mudah Menjumlahkan Bilangan Heksadesimal
Hey guys, kali ini penulis ingin menjelaskan tentang cara mudah menjumlahkan bilangan heksadesimal, oke kita langsung ke pembahasannya saja. Pada umumnya, menyelesaikan operasi penjumlahan pada bilangan heksadesimal adalah dengan cara mengkonversinya dahulu ke dalam desimal baru kemudian kita jumlahkan dan dikonversikan lagi ke dalam bilangan heksadesimal, jika bilangannya kecil mungkin masih mudah, tetapi bagaimana jika bilangannya relatif besar, pasti agak sedikit sulit mengkonversinya. Maka dari itu penulis menemukan cara mudah menghitungnya tanpa perlu repot - repot mengkonversinya terlebih dahulu. Metodenya cukup simple penulis menamainya "Metode Pisah".
Sebelum membahas contoh soalnya, pertama kali yang harus dipahami disini adalah aturannya, jika sudah memahami aturannya dijamin pasti mudah dalam menjumlahkannya.
Aturan :
Misalkan ada dua buah bilangan a dan b, yang memenuhi operasi a + b, maka a + b dapat dijumlah langsung kecuali jika b adalah huruf misal A, B, C, D, E, dan F, maka aturannya :
- A = 4 apabila b > 5
- B = 5 apabila b > 4
- C = 6 apabila b > 3
- D = 7 apabila b > 2
- E = 8 apabila b > 1
- F = 9 apabila b > 0
Note: Apabila kondisinya keduanya huruf, maka boleh diganti salah satunya.
Contoh 1 :
Jumlahkan 1C3 dengan 3D !
Jawab :
1C3 + 3D = 1|C|3 + 0|3|D
= 1+0|C+3|3+D
* 3+D = D+3, karena b = 3 sementara untuk D syaratnya b > 2, maka D = 7. Sehingga :
3+D = D+3 = 7+3 = 10
1C3+3D = 1|C|3+0|3|D
= 1+0|C+3+1|0 (1 karena D+3 = 10 simpan 1)
= 1+0|C+4|0
* C+4, karena 4 > 3, maka C = 6. Sehingga :
C+4 = 6+4 = 10
1C3 + 3D = 1|C|3 + 3|D
= 1+0+1|0|0
= 2|0|0 = 200
Jadi, 1C3 + 3D = 200.
Contoh 2: Apabila keduanya huruf
AD + 1C = ...
Jawab:
AD+1C = A|D + 1|C
= A + 1|D + C
* D+C, karena a atau b huruf, maka bisa diganti salah satu, misal penulis ingin mengganti b, maka perlu dilihat syarat yang ketiga, diperoleh C = 6, sementara untuk D kita ganti dengan desimalnya yaitu 13. Jadi :
D+C = 13+6 = 19
AD + 1C = A|D + 1|C
= A+1+1|9
= A+2|9 = C|9 = C9
Coba bandingkan hasilnya dengan cara pada umumnya, sebenarnya biar lebih enak dibuat seperti penjumlahan bersusun kebawah. Bagaimana ? Mudah bukan caranya silahkan dicoba sendiri yah, terima kasih.
Hey guys, kali ini penulis ingin menjelaskan tentang cara mudah menjumlahkan bilangan heksadesimal, oke kita langsung ke pembahasannya saja. Pada umumnya, menyelesaikan operasi penjumlahan pada bilangan heksadesimal adalah dengan cara mengkonversinya dahulu ke dalam desimal baru kemudian kita jumlahkan dan dikonversikan lagi ke dalam bilangan heksadesimal, jika bilangannya kecil mungkin masih mudah, tetapi bagaimana jika bilangannya relatif besar, pasti agak sedikit sulit mengkonversinya. Maka dari itu penulis menemukan cara mudah menghitungnya tanpa perlu repot - repot mengkonversinya terlebih dahulu. Metodenya cukup simple penulis menamainya "Metode Pisah".
Sebelum membahas contoh soalnya, pertama kali yang harus dipahami disini adalah aturannya, jika sudah memahami aturannya dijamin pasti mudah dalam menjumlahkannya.
Aturan :
Misalkan ada dua buah bilangan a dan b, yang memenuhi operasi a + b, maka a + b dapat dijumlah langsung kecuali jika b adalah huruf misal A, B, C, D, E, dan F, maka aturannya :
- A = 4 apabila b > 5
- B = 5 apabila b > 4
- C = 6 apabila b > 3
- D = 7 apabila b > 2
- E = 8 apabila b > 1
- F = 9 apabila b > 0
Note: Apabila kondisinya keduanya huruf, maka boleh diganti salah satunya.
Contoh 1 :
Jumlahkan 1C3 dengan 3D !
Jawab :
1C3 + 3D = 1|C|3 + 0|3|D
= 1+0|C+3|3+D
* 3+D = D+3, karena b = 3 sementara untuk D syaratnya b > 2, maka D = 7. Sehingga :
3+D = D+3 = 7+3 = 10
1C3+3D = 1|C|3+0|3|D
= 1+0|C+3+1|0 (1 karena D+3 = 10 simpan 1)
= 1+0|C+4|0
* C+4, karena 4 > 3, maka C = 6. Sehingga :
C+4 = 6+4 = 10
1C3 + 3D = 1|C|3 + 3|D
= 1+0+1|0|0
= 2|0|0 = 200
Jadi, 1C3 + 3D = 200.
Contoh 2: Apabila keduanya huruf
AD + 1C = ...
Jawab:
AD+1C = A|D + 1|C
= A + 1|D + C
* D+C, karena a atau b huruf, maka bisa diganti salah satu, misal penulis ingin mengganti b, maka perlu dilihat syarat yang ketiga, diperoleh C = 6, sementara untuk D kita ganti dengan desimalnya yaitu 13. Jadi :
D+C = 13+6 = 19
AD + 1C = A|D + 1|C
= A+1+1|9
= A+2|9 = C|9 = C9
Coba bandingkan hasilnya dengan cara pada umumnya, sebenarnya biar lebih enak dibuat seperti penjumlahan bersusun kebawah. Bagaimana ? Mudah bukan caranya silahkan dicoba sendiri yah, terima kasih.
Rabu, 13 Mei 2020
Sejarah Ilmuwan Matematika Islam Dalam Bidang Kalkulus
A. Pengertian Kalkulus
Kalkulus berasal dari bahasa Latin, calculus, yang berarti batu kecil. Kalkulus merupakan cabang ilmu matematika yang mencakup limit, turunan, integral, dan deret tak terhingga.
Kalkulus mempunyai aplikasi yang luas dalam bidang sains dan teknik dan digunakan untuk memecahkan masalah yang kompleks--aljabar tidak cukup untuk menyelesaikannya.
B. Sejarah Penemu Islam Kalkulus
Ahli matematika Islam yang berperan untuk mengkaji kalkulus adalah al-Karaji. Sejarawan matematika F Woepcke memuji al-Karaji karena dianggap sebagai ilmuwan pertama yang memperkenalkan teori kalkulus aljabar. Setelah itu, Ibn al-Haytham atau yang dikenal sebagai al-Hazen di Barat juga ikut berkontribusi dalam menghasilkan rumus terkait kalkulus yaitu memperoleh jumlah kekuatan keempat. Dia menggunakan hasil untuk melakukan apa yang sekarang disebut integrasi, di mana rumus untuk jumlah kuadrat integral jumlah kekuatan keempat memungkinkan dia untuk menghitung volume parabola. Pada abad ke-12, ahli matematika Persia, Sharaf al-Din al-Tusi, juga tercatat sebagai penemu turunan polynominal kubik sebuah hasil yang penting dalam diferensial kalkulus.
Al Karaji
Ibn al-Haytham
Selasa, 05 Mei 2020
Riwayat Singkat Penulis
Penulis lahir pada tanggal 15 Januari 1997 dan merupakan anak kedua dari tiga bersaudara, saudara yang pertama bernama Reski Pratama, STP dan saat ini sedang bekerja di perusahaan Zenius , Kemudian saudara yang terakhir bernama Nabila Aliya Ramadhani yang saat ini sedang kuliah di UNIB mengambil jurusan Pendidikan Guru Sekolah Dasar. Penulis sangat suka bermain catur dan game yang membangun base dan memakai strategi misalnya Age Of Empires, Command and Conquer, dll. Tetapi lebih tertarik kepada matematika.
Riwayat Pendidikan
Penulis pernah menempuh sekolah dasar di SDN 20 Pagi Jakarta Timur bahkan sempat tidak naik kelas setahun kemudian, pada tahun 2011 penulis menempuh pendidikan SMP di SMPN 232 Jakarta tetapi hanya sebatas kelas VII dan saat kelas VIII pindah sekolah ke SMPN 2 Curup Timur kemudian dinyatakan lulus pada tahun 2013. Kemudian penulis melanjutkan pendidikan di SMA XAVERIUS CURUP pada tahun yang sama dan lulus pada tahun 2016. Setelah penulis dinyatakan lulus, penulis melanjutkan studi di perguruan tinggi islam yaitu di IAIN CURUP mengambil jurusan pendidikan matematika sampai sekarang.
Penulis lahir pada tanggal 15 Januari 1997 dan merupakan anak kedua dari tiga bersaudara, saudara yang pertama bernama Reski Pratama, STP dan saat ini sedang bekerja di perusahaan Zenius , Kemudian saudara yang terakhir bernama Nabila Aliya Ramadhani yang saat ini sedang kuliah di UNIB mengambil jurusan Pendidikan Guru Sekolah Dasar. Penulis sangat suka bermain catur dan game yang membangun base dan memakai strategi misalnya Age Of Empires, Command and Conquer, dll. Tetapi lebih tertarik kepada matematika.
Riwayat Pendidikan
Penulis pernah menempuh sekolah dasar di SDN 20 Pagi Jakarta Timur bahkan sempat tidak naik kelas setahun kemudian, pada tahun 2011 penulis menempuh pendidikan SMP di SMPN 232 Jakarta tetapi hanya sebatas kelas VII dan saat kelas VIII pindah sekolah ke SMPN 2 Curup Timur kemudian dinyatakan lulus pada tahun 2013. Kemudian penulis melanjutkan pendidikan di SMA XAVERIUS CURUP pada tahun yang sama dan lulus pada tahun 2016. Setelah penulis dinyatakan lulus, penulis melanjutkan studi di perguruan tinggi islam yaitu di IAIN CURUP mengambil jurusan pendidikan matematika sampai sekarang.
Langganan:
Komentar (Atom)